Árboles

Objetivos

• Entender los conceptos básicos de los árboles y su estructura jerárquica.

• Aprender las características y tipos de árboles utilizados en programación.

• Conocer aplicaciones prácticas de los árboles en informática.

• Implementar árboles en Java con ejemplos detallados.

Introducción

Los árboles son estructuras de datos fundamentales en informática, utilizadas para organizar y gestionar información de una manera eficiente y jerárquica. Debido a su capacidad para almacenar datos de forma ordenada, son comunes en aplicaciones como sistemas de archivos, bases de datos, y algoritmos de inteligencia artificial. En esta clase exploraremos sus conceptos básicos, características, tipos, y una implementación práctica en Java.

Los árboles son considerados una estructura de datos no lineales. Estas estructuras suponen un gran avance en la organización de datos, ya que nos permiten implementar un gran número de algoritmos mucho más rápido que cuando utilizamos estructuras de datos lineales, como arrays o listas enlazadas. Los árboles también ofrecen una organización natural de los datos, por lo que se han convertido en estructuras omnipresentes en sistemas de archivos, interfaces gráficas de usuario, bases de datos, sitios web y muchos otros sistemas informáticos.

Cuando se dice que los árboles son «no lineales», se refiere a una relación organizativa más rica que las simples relaciones «antes» y «después» entre objetos en secuencias. Las relaciones en un árbol son jerárquicas: algunos objetos están «por encima» y otros «por debajo» de otros. En realidad, la terminología principal de las estructuras de datos en árbol procede de los árboles genealógicos, siendo los términos padre, hijo, antepasado y descendiente los más utilizados para describir las relaciones. Uno de los ejemplos más claros es la estructura de archivos de linux (comando tree hace algo similar).

Definición Formal

Formalmente, definimos un árbol T como un conjunto de nodos que almacenan elementos tales que los nodos tienen una relación padre-hijo que satisface las siguientes propiedades:

• Si T no es vacío, tiene un nodo especial, llamado raíz de T , que no tiene padre.

• Cada nodo v de T distinto de la raíz tiene un único nodo padre w; cada nodo con padre w es hijo de w.

Obsérvese que, según nuestra definición, un árbol puede estar vacío, es decir, no tener ningún nodo. Esta convención también nos permite definir un árbol de forma recursiva, de modo que un árbol T está vacío o consta de un nodo r, denominado raíz de T, y un conjunto (posiblemente vacío) de subárboles cuyas raíces son los hijos de r.

Conceptos Básicos

Un árbol es una estructura de datos no lineal que organiza los datos de manera jerárquica. Un árbol está compuesto por nodos conectados entre sí, donde cada nodo puede tener hijos y un único padre, salvo el nodo raíz, que es el nodo inicial sin padre.

Cada nodo de un árbol contiene tres elementos fundamentales:

1. Dato: el valor o información que almacena el nodo.

2. Nodo Padre: el nodo que está un nivel arriba en la jerarquía (excepto el nodo raíz).

3. Nodos Hijos: los nodos que dependen de él en la jerarquía.

4. Jerarquía: La organización de los datos es jerárquica, similar a una estructura de organización en una empresa.

5. Conexiones Únicas: Cada nodo, excepto el raíz, tiene un solo padre.

6. Subárboles: Cualquier nodo puede servir como raíz de su propio subárbol.

7. Recorridos Múltiples: Los árboles pueden recorrerse en diferentes órdenes (preorden, inorden y postorden).

Otros términos que se suelen utilizar son:

• Un nodo u es antepasado de un nodo v si u = v o u es antepasado del padre de v.

• Un nodo v es descendiente de un nodo u si u es antepasado de v.

• El subárbol de T enraizado en un nodo v es el árbol formado por todos los descendientes de v en T (incluido el propio v).

• Una arista del árbol T es un par de nodos (u, v) tal que u es el padre de v, o viceversa.

• Un camino de T es una secuencia de nodos tal que dos nodos consecutivos cualesquiera de la secuencia forman una arista.

Propiedades

Un árbol es una estructura de datos jerárquica con las siguientes propiedades:

• Raíz: el nodo principal o raíz del árbol es el punto de inicio de la estructura, y no tiene padres.

• Nodos Internos: nodos que tienen al menos un hijo.

• Padre: Nodo que tiene conexiones hacia uno o más nodos hijos.

• Hijo: Nodo que tiene un nodo padre.

• Hoja: Nodo sin hijos.

• Nivel: Profundidad de un nodo en relación con la raíz.

• Altura del Árbol: la distancia máxima de la raíz a una hoja.

• Profundidad: número de niveles desde el nodo raíz hasta un nodo específico.

• Grafo Conectado: todos los nodos están interconectados sin ciclos, es decir, no hay bucles en la estructura.

Figura 46 Elementos de un árbol. Imagen tomada de Applications of tree data structure - Geeksforgeeks.

Representación Gráfica

Un árbol de ejemplo puede verse así:

        A (Raíz)
       / \
      B   C
     / \   \
    D   E   F

En este caso:

• A es la raíz.

• D, E, y F son nodos hoja.

• La altura es 2.

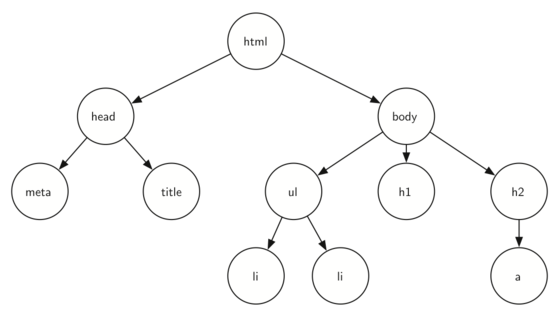
Figura 47 Ejemplo de árbol correspondiente a los elementos de marcado de una página web. Tomado de 7.2. Examples of Trees.

Visualización

Herramientas para visualizar árboles:

• BSTeBook

• Graphonline

• Clase BSTAnimation.java del libro guía [8].

Tipos de Árboles

Figura 48 Tipos de árbol según hijos. Imagen tomada de Types of Trees in Data Structures - Geeksforgeeks.

• Árbol Binario: Cada nodo tiene un máximo de dos hijos.

• Árbol Binario de Búsqueda (BST): Árbol binario donde el valor del hijo izquierdo es menor que el del nodo padre, y el valor del hijo derecho es mayor.

• Árbol AVL: Árbol binario de búsqueda balanceado, donde la diferencia de altura entre los subárboles de cada nodo es a lo sumo uno.

• Árbol Rojo-Negro: Un BST balanceado que mantiene restricciones adicionales sobre la profundidad de los nodos.

• Árbol N-ario: Cada nodo puede tener un número máximo de N hijos.

• Árbol B: un árbol de búsqueda de grado múltiple utilizado en bases de datos y sistemas de archivos, donde cada nodo puede tener más de dos hijos.

Binario de Búsqueda (BST)

Un árbol binario es un árbol ordenado con las siguientes propiedades:

1. Cada nodo tiene como máximo dos hijos.

2. Cada nodo hijo se etiqueta como hijo izquierdo o hijo derecho.

3. Un hijo izquierdo precede a un hijo derecho en el orden de los hijos de un nodo.

El subárbol enraizado en un hijo izquierdo o derecho de un nodo interno v se denomina subárbol izquierdo o subárbol derecho, respectivamente, de v. Un árbol binario es propio si cada nodo tiene cero o dos hijos. Algunas personas también se refieren a este tipo de árboles como árboles binarios completos. Así, en un árbol binario correcto, cada nodo interno tiene exactamente dos hijos. Un árbol binario que no es propio es impropio.

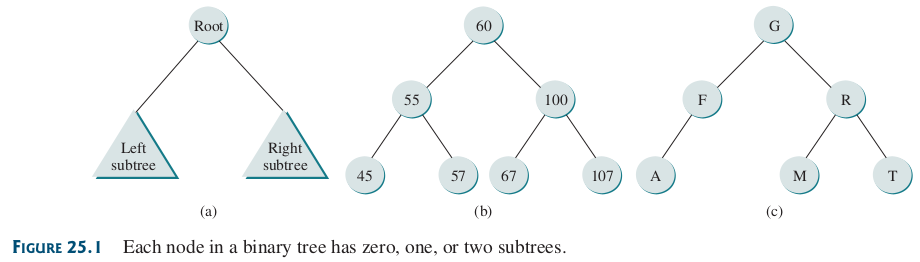
Figura 49 Ejemplos de nodos binarios.

Por lo tanto, para cada nodo de un árbol de búsqueda binario, el valor de su hijo izquierdo es menor que el valor del nodo, y el valor de su hijo derecho es mayor que el valor del nodo. Entonces, ¿qué ventajas tienen árboles binarios? Un árbol de búsqueda binario es más eficaz que una lista para las operaciones de búsqueda, inserción y eliminación.

Crear el diagrama del árbol de la imagen parte (b). Para ello utilicen cualquier herramienta de la sección de Visualización.

Aplicaciones

Los árboles son versátiles y se utilizan en muchas aplicaciones:

• Sistemas de archivos: Organizan archivos y carpetas en jerarquías.

• Bases de datos: Estructuras como B-trees y AVL trees se emplean en índices de bases de datos para búsquedas rápidas.

• Compiladores: Utilizan árboles de sintaxis abstracta para interpretar el código.

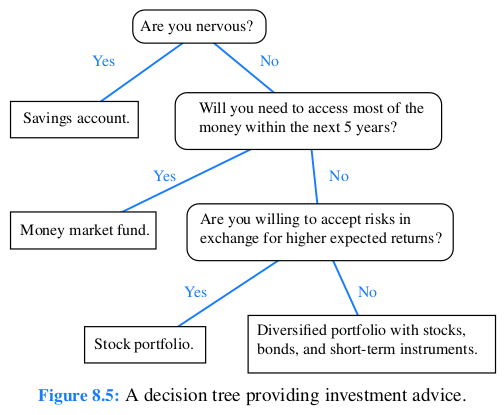
• Inteligencia Artificial: Se aplican en algoritmos de toma de decisiones, como los árboles de decisión.

• Redes: Representan rutas en protocolos de redes y otros sistemas jerárquicos.

Ejemplos

Árboles No Binario

Los árboles se aplican ampliamente en situaciones reales que requieren organizar datos de forma jerárquica o rápida recuperación. En bases de datos, los árboles B y B+ se usan para indexar datos, permitiendo búsquedas y accesos eficientes. En sistemas operativos, los árboles de directorios representan la estructura de archivos y carpetas, facilitando la navegación. Además, en inteligencia artificial, los árboles de decisión ayudan a clasificar y tomar decisiones basadas en datos, y en redes, los árboles de enrutamiento optimizan la transmisión de paquetes entre dispositivos en la red.

Figura 50 Árbol genealógico.

Figura 51 Estructura de una organización.

Figura 52 Sistema operativo.

Figura 53 Estructura de un libro.

Árboles Binarios

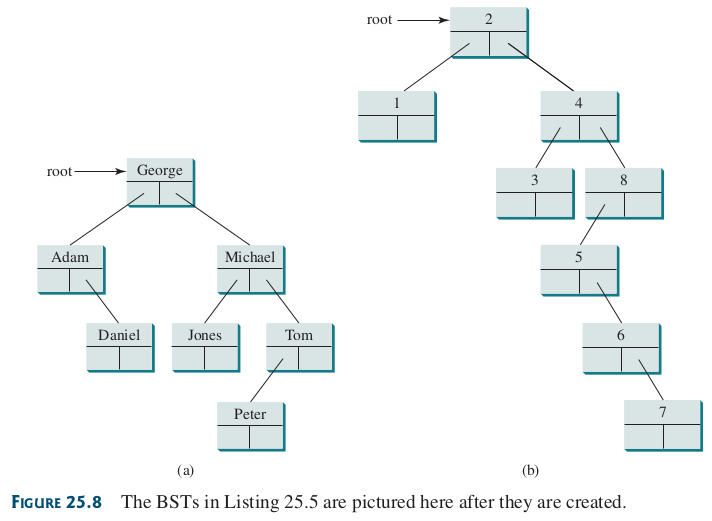
Figura 54 Árbol binario de números y letras.

Figura 55 Preguntas y respuestas binarias.

Figura 56 Expresiones matemáticas.

Recorridos

Depth-First Search (DFS)

En español búsqueda en profundidad o búsqueda exhaustiva.

En este tipo de recorrido se divide el árbol en tres sub-árboles: raíz o director (<dir> o <root>), izquierda (<left>), y derecha (<right>). Dependiendo del tipo de recorrido se define el orden en que se recorre.

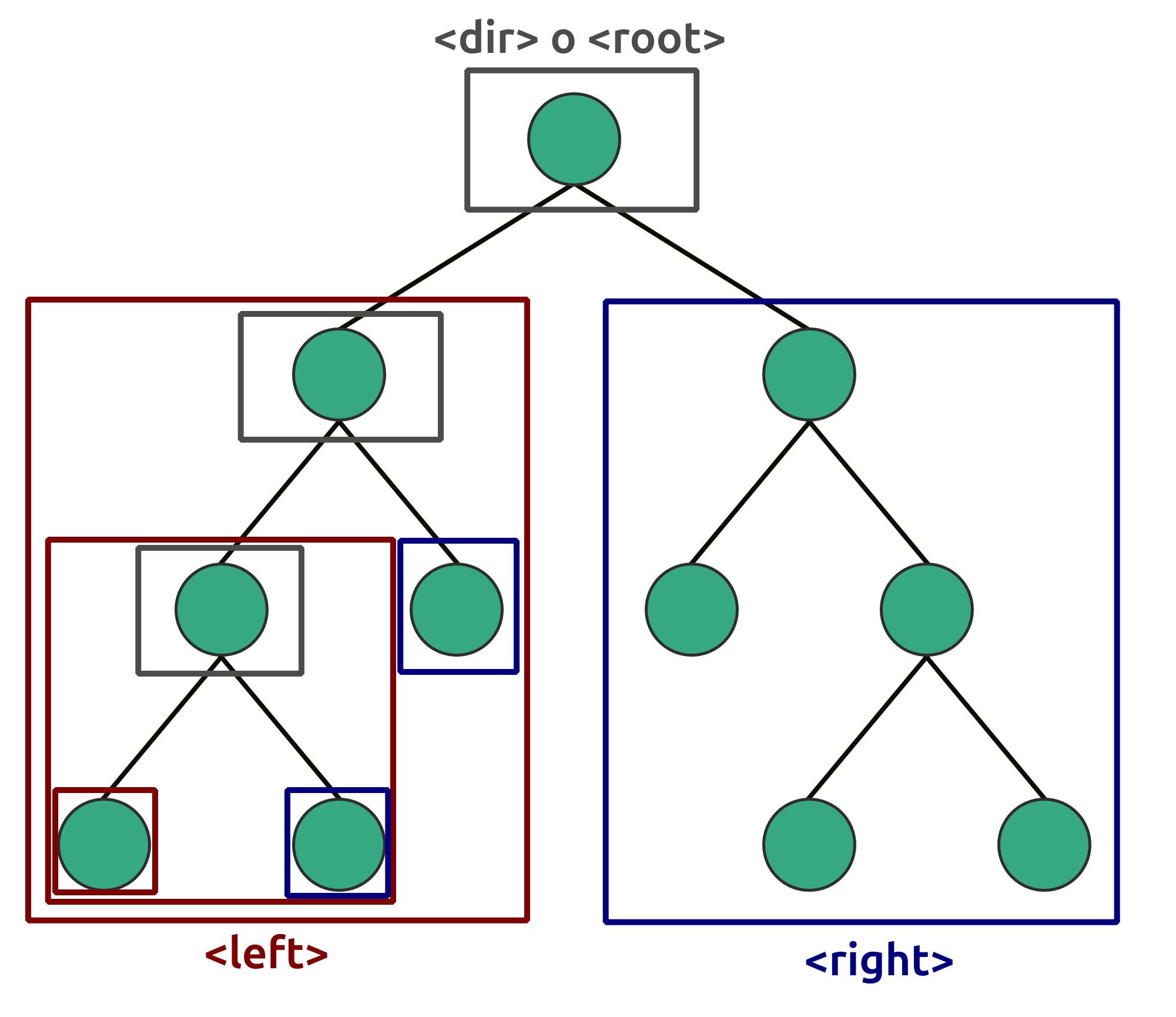
Figura 57 Sub-árboles utilizados para recorrer un árbol de forma DFS.

Pre-Order

Orden

<dir> - <left> - <right>

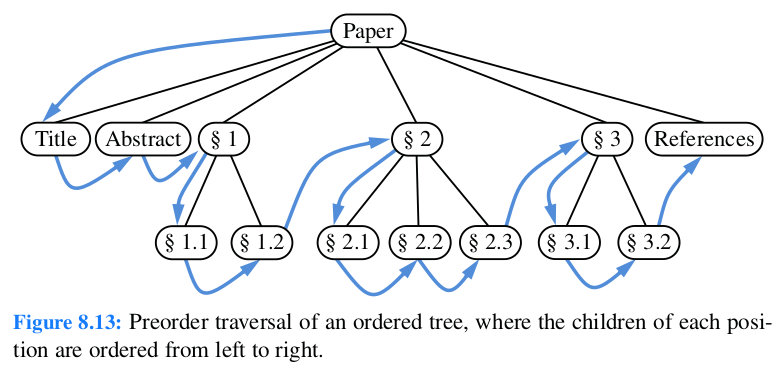
Figura 58 Ejemplo recorrido preorden para un grafo que representa la estructura de un libro.

In-Order

Orden

<left> - <dir> - <right>

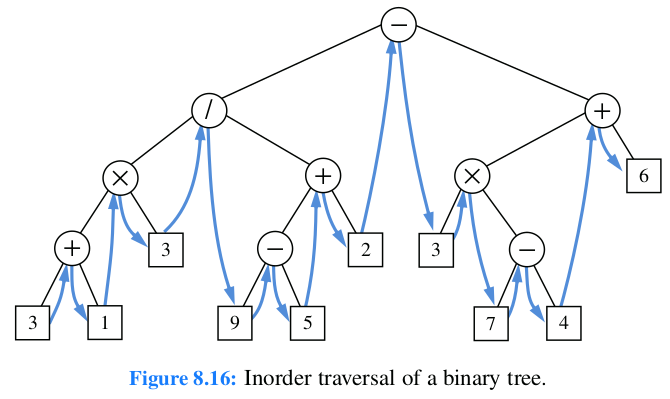
Figura 59 Ejemplo recorrido en orden para un grafo que representa la estructura de un libro.

Post-Order

Orden

<left> - <right> - <dir>

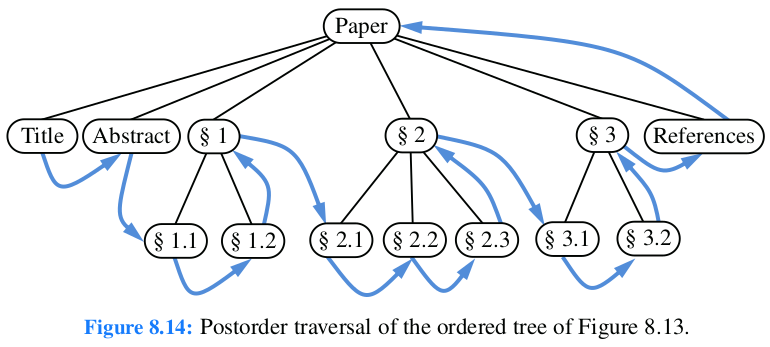
Figura 60 Ejemplo recorrido Post-Order para un grafo que representa la estructura de un libro.

Ejemplo General

Figura 61 Todos los recorridos de un árbol. Pre-order: verde, In-order: verde, Post-Order: azul. Tomado de Wikipedia, Tree traversal .

Recorrido en profundidad (camino punteado) de un árbol binario:

• Pre-Order previo (nodo visitado en la posición roja): F, B, A, D, C, E, G, I, H

• In-Order (nodo visitado en posición verde): A, B, C, D, E, F, G, H, I

• Post-Order (nodo visitado en la posición azul): A, C, E, D, B, H, I, G, F

Breadth-First Search (BFS)

En español búsqueda general o búsqueda por amplitud. También suele llamarse como Level Order

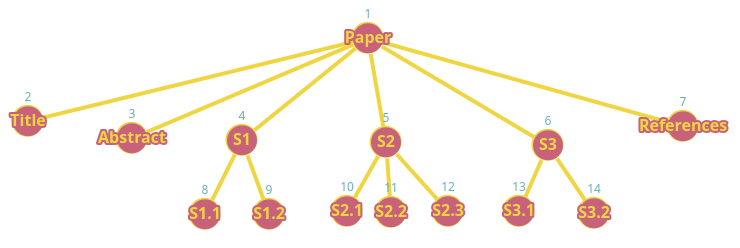
Figura 62 Ejemplo recorrido en búsqueda por amplitud para un grafo que representa la estructura de un libro.

Tour de Euler

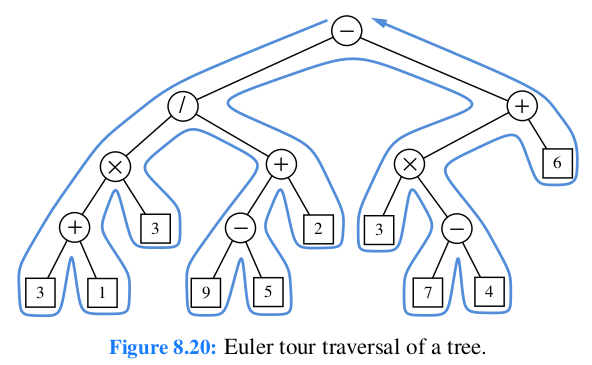
Figura 63 Ejemplo de recorrido general, también conocido como Tour de Euler.

Implementación en Java

Simple

Un árbol de búsqueda binario puede implementarse utilizando una estructura enlazada, es decir, puede representarse mediante un conjunto de nodos enlazados. Cada nodo contiene un valor y dos enlaces denominados izquierda y derecha que hacen referencia al hijo izquierdo y al hijo derecho.

// Clase simpla de un árbol binario
class TreeNode<E> {
  protected E element;
  protected TreeNode<E> left;
  protected TreeNode<E> right;

  public TreeNode(E e) {
      element = e;
  }
}

TreeNode<Integer> nodo_numeros = new TreeNode<>(60);
// primer nivel
nodo_numeros.left = new TreeNode<>(55);
nodo_numeros.right = new TreeNode<>(100);
// segundo nivel
nodo_numeros.left.left = new TreeNode<>(45);
nodo_numeros.left.right = new TreeNode<>(57);

nodo_numeros.right.left = new TreeNode<>(67);
nodo_numeros.right.right = new TreeNode<>(107);

System.out.println(nodo_numeros.right.right.element)

107

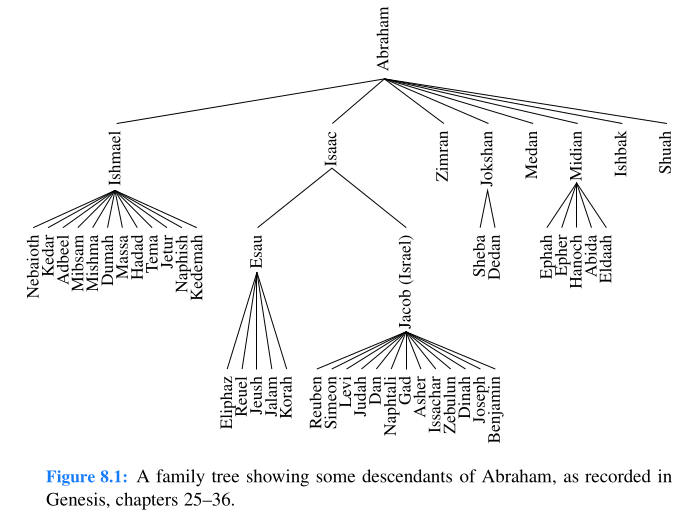
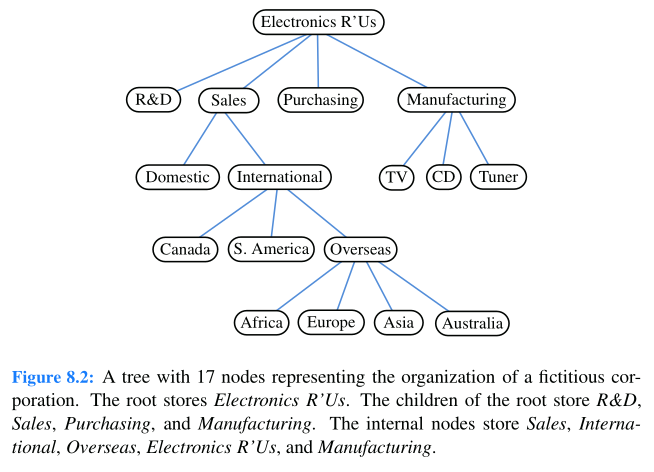
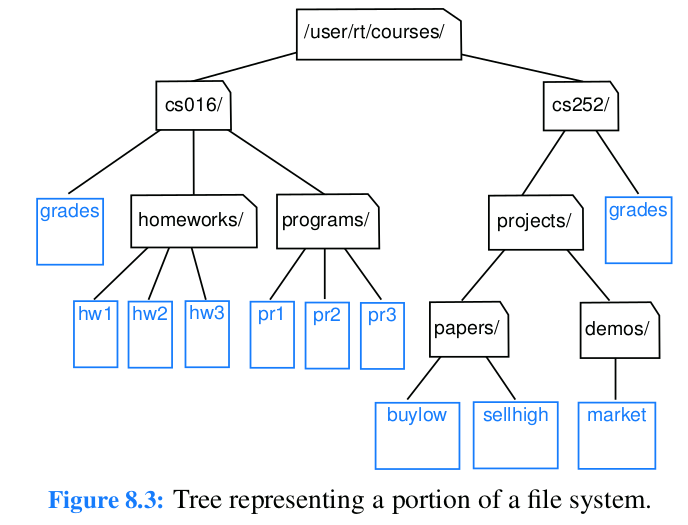
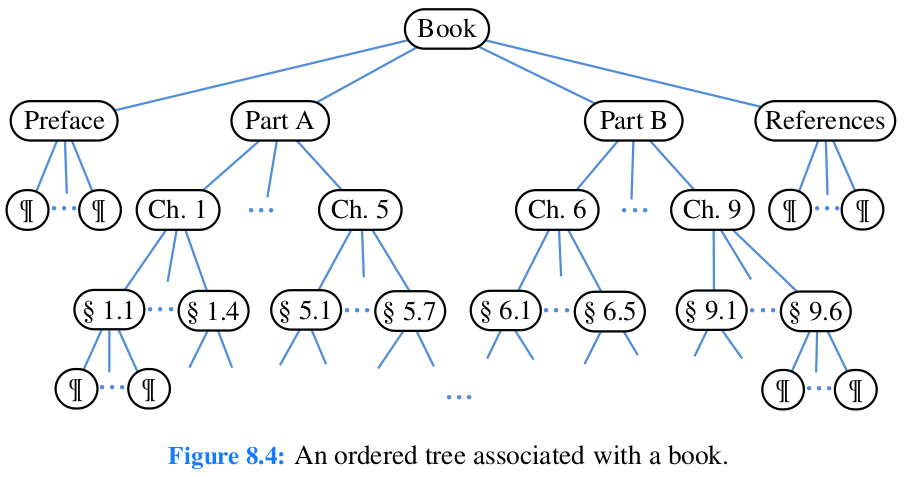
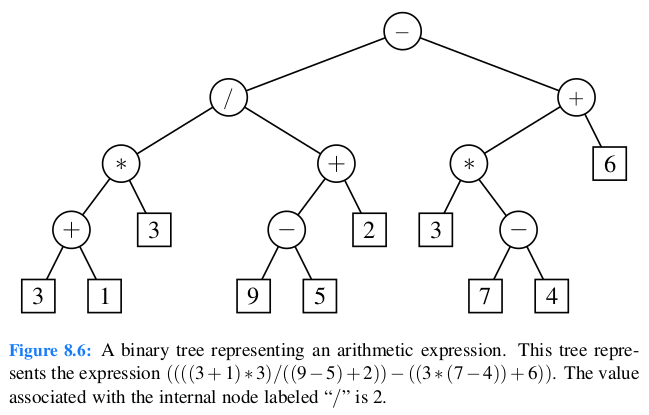
Implementa el árbol de las Figuras 8.3, 8.4, 25.5 y 25.8, utilizando la clase TreeNode .

// Agregar código aquí

Árbol Binario de Búsqueda (BST)

A continuación, implementaremos un árbol binario de búsqueda (BST), uno de los tipos de árboles más comunes en estructuras de datos. Esta clase incluye métodos para insertar, buscar y recorrer el árbol en diferentes órdenes.

Además, la clase ArbolBinario utiliza nodos, cada nodo del árbol contiene un valor y referencias a sus hijos izquierdo y derecho.

class Nodo {
    int valor;
    Nodo izquierdo, derecho;

    public Nodo(int valor) {
        this.valor = valor;
        izquierdo = derecho = null;
    }
}

public class ArbolBinario {
  Nodo raiz;

  // Constructor
  public ArbolBinario() {
      raiz = null;
  }

  // Método para insertar un nuevo nodo en el árbol
  public void insertar(int valor) {                                 
      raiz = insertarRecursivo(raiz, valor);
  }

  private Nodo insertarRecursivo(Nodo raiz, int valor) {
      if (raiz == null) {
          raiz = new Nodo(valor);
          return raiz;
      }
      if (valor < raiz.valor) {
          raiz.izquierdo = insertarRecursivo(raiz.izquierdo, valor);
      } else if (valor > raiz.valor) {
          raiz.derecho = insertarRecursivo(raiz.derecho, valor);
      }
      return raiz;
  }

  // Método para buscar un nodo en el árbol
  public boolean buscar(int valor) {
      return buscarRecursivo(raiz, valor);
  }

  private boolean buscarRecursivo(Nodo raiz, int valor) {
      if (raiz == null) {
          return false;
      }
      if (valor == raiz.valor) {
          return true;
      }
      return valor < raiz.valor ? buscarRecursivo(raiz.izquierdo, valor) : buscarRecursivo(raiz.derecho, valor);
  }

  // Método para recorrido en inorden
  public void recorridoInorden() {
      recorridoInordenRecursivo(raiz);
  }

  private void recorridoInordenRecursivo(Nodo raiz) {
      if (raiz != null) {
          recorridoInordenRecursivo(raiz.izquierdo);
          System.out.print(raiz.valor + " ");
          recorridoInordenRecursivo(raiz.derecho);
      }
  }

  // Método para recorrido en preorden
  public void recorridoPreorden() {
      recorridoPreordenRecursivo(raiz);
  }

  private void recorridoPreordenRecursivo(Nodo raiz) {
      if (raiz != null) {
          System.out.print(raiz.valor + " ");
          recorridoPreordenRecursivo(raiz.izquierdo);
          recorridoPreordenRecursivo(raiz.derecho);
      }
  }

  // Método para recorrido en postorden
  public void recorridoPostorden() {
      recorridoPostordenRecursivo(raiz);
  }

  private void recorridoPostordenRecursivo(Nodo raiz) {
      if (raiz != null) {
          recorridoPostordenRecursivo(raiz.izquierdo);
          recorridoPostordenRecursivo(raiz.derecho);
          System.out.print(raiz.valor + " ");
      }
  }
}

Prueba la clase en la siguiente casilla, implementa el árbol en las Figuras: Figura 51, Figura 52, Figura 54, y Figura 66.

// Agregar código aquí

Nivel Medio

Implementar el árbol del repositorio Data-Structures-Algorithms-Java/Non Linear Data Structures/Trees - indraantoor -Github. Como esta clase esta pensada para ejecutarla por fuera de notebooks, shell, para ejecutarla desde el notebook deben sacar la

// Agregar código aquí

Probar esta clase implementando alguna de las Figuras Figura 51, Figura 52, Figura 54, y Figura 66.

// Probar clase aquí

Robusta y Completa

Interfaz y Clase Árbol

Implementa la interfaz Tree.java del libro guía [8]. Listing 25.3, capítulo 25, página cmlxxxix.

Figura 64 Diagrama de clases de la interfaz genérica Graph.

// Tree.java

Ahora, implementa el código de BST.java, Binary Search Trees (BST). Listing 25.4, capítulo 25, página cmxci.

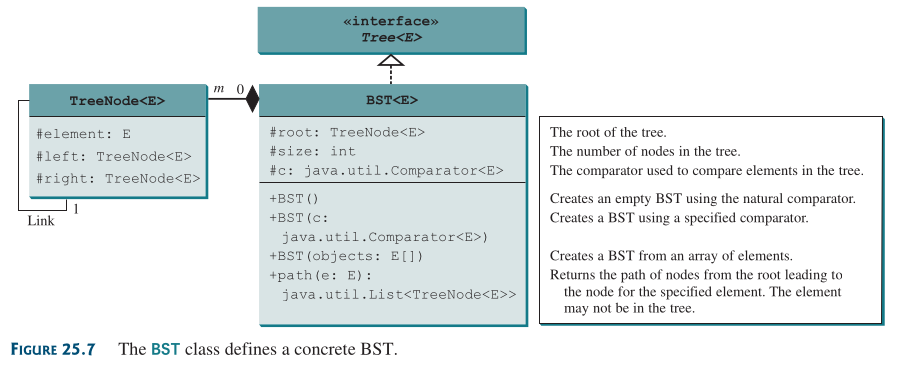
Figura 65 Diagrama de clase de la clase TreeNode y BST.

BST es iterable porque está definido como un subtipo de la interfaz java.lang.Iterable.

// BST.java

Ahora, implementa la clase de prueba TestBST.ava del libro guía. Listing 25.5, capítulo 25, página cmxcvi.

Esta clase implementa una solución a la estructura de la siguiente image:

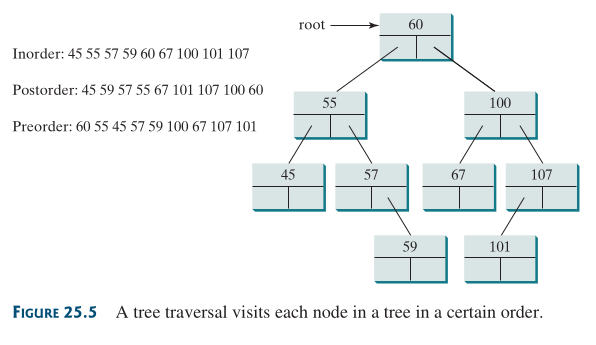
Figura 66 Árbol binario de números enteros organizados.

// Ingresar código aquí

¿Cómo se eliminan elementos de un árbol? Implementa y prueba la clase TestBSTDelete.java del libro guía. Listing 25.7, capítulo 25, página m.

// TestBSTDelete.java

Ahora, implementemos la clase para iterar sobre un árbol BTS, TestBSTWithIterator.java, Listing 25.10, capítulo 25, página mvii.

BST es iterable porque está definido como un subtipo de la interfaz java.lang.Iterable.

// TestBSTWithIterator.java

Ejercicio

Taller 6

Realizar las siguientes tareas y respondan las preguntas realizadas:

• Implementar los árboles de las Figuras: Figura 51 y Figura 52, utilizando la clase de nivel Medio. ¿Se pueden implementar estos árboles con la clase Robusta? Además, realizar los recorridos BFS y DFS: In-Order, Pre-Order, y Post-Order.

• Implementar los árboles de las Figuras: Figura 54 y Figura 66, utilizando la clase Robusta. ¿Qué diferencias hay con las demás clases, ventajas/desventajas? Además, realizar los recorridos BFS y DFS: In-Order, Pre-Order, y Postorder.

• Dibujar los diagramas en cualquier herramienta mencionada en la sección de Visualización. Pueden utilizar el código de la siguiente tarea.

• Implementar la clase BSTAnimation.java del libro guía [8] para visualizar los árboles binarios. Recuerden que para poder ejecutar esta clase se necesitan javaFX y crear un proyecto de java con Maven que sea de arquetipo JavaFX.

Importante

El trabajo se debe entregar como un proyecto de java. Deben subir la carpeta del proyecto comprimida en formato .zip o .tar. Pueden trabajar en parejas, pero cada uno debe presentar todo.

Conclusión

Los árboles son una estructura de datos esencial en programación y se aplican en diversas áreas de la informática. Al comprender los conceptos teóricos y poner en práctica la implementación de árboles en Java, se obtiene una herramienta poderosa para la manipulación y organización de datos complejos de manera jerárquica.

Recursos Adicionales

Guías y Tutoriales

• Tree Traversal Techniques

• Binary Search Tree Traversal – Inorder, Preorder, Post Order for BST

• Tree traversal - Wikipedia

• Binary Search Tree (BST) Traversals – Inorder, Preorder, Post Order

• Tree Data Structure - JavatPoint

• DSA using Java - Tree

• Tree Data Structure with Java

Videos

• Simplest Binary Tree Traversal trick for preorder inorder postorder

• Binary tree traversal - breadth-first and depth-first strategies