Sin Peso#
Introducción#
Los grafos sin peso son una estructura de datos fundamental en ciencias de la computación y matemáticas, utilizada para modelar relaciones entre objetos de manera simple. A diferencia de los grafos ponderados, en los grafos sin peso no se asigna un valor cuantitativo a las aristas; solo se representa la existencia de una conexión entre dos nodos. Este tipo de grafos es ideal para problemas donde las relaciones son cualitativas o donde el costo de las conexiones no es relevante, como en redes sociales, sistemas de recomendación y exploración de grafos.
Su simplicidad los convierte en una herramienta versátil para resolver problemas como el cálculo de caminos mínimos (usando algoritmos como BFS o DFS), la detección de ciclos, y la verificación de conectividad entre nodos. En esta clase, exploraremos las propiedades, aplicaciones y métodos de implementación de grafos sin peso, destacando su importancia en diversas áreas como informática, biología y ciencias sociales.
Ejemplos#
Ciudades de Colombia#
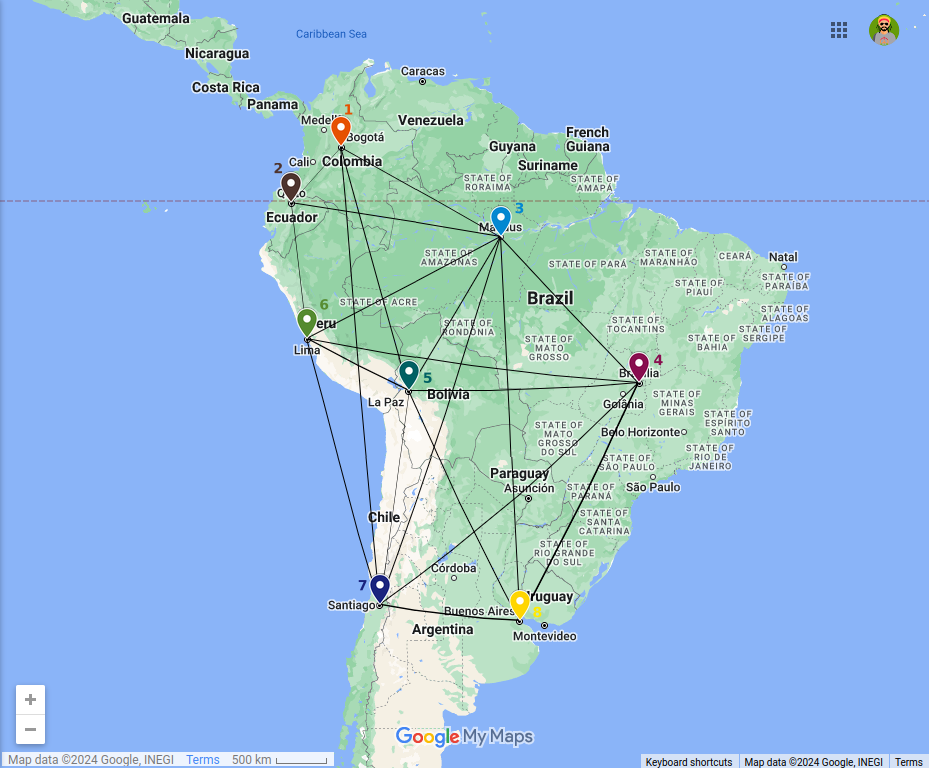
Figura 69 Ejemplo de grafo para representar vuelos entre ciudades de Colombia.#
Ciudades de EEUU#
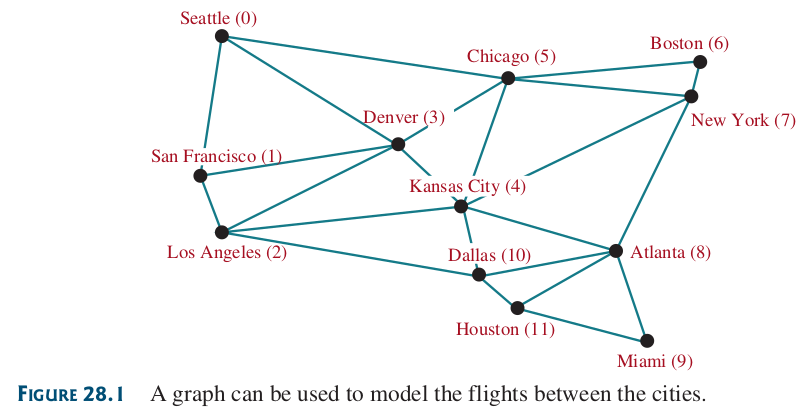
Figura 70 Ejemplo de grafo representando vuelos entre diferentes ciudades.#
Terminología de Grafos#
Conceptos Básicos#
Vértices o Nodos: Elementos individuales que componen el grafo.
Aristas o Enlaces: Conexiones entre nodos.
Grafo Dirigido: Un grafo donde las aristas tienen dirección.
Grafo No Dirigido: Un grafo donde las aristas no tienen dirección, y la conexión es bidireccional.
Peso de Arista: Un valor numérico asociado a una arista que puede representar distancia, costo, etc.
Camino: Secuencia de nodos donde cada par consecutivo de nodos está conectado por una arista.
Ciclo: Camino cerrado en el cual el nodo inicial y final son el mismo.
Conectividad: Propiedad que indica si existe un camino entre cada par de nodos.
Grafo Completo: Grafo en el cual todos los nodos están conectados entre sí.
Definición Formal#
Dicho de otra forma. Un gráfico es una estructura matemática que representa relaciones entre entidades del mundo real. Por ejemplo, el grafo de la Figura 70 representa los vuelos entre ciudades, y el grafo de la Figura 68(b) representa los puentes entre masas de tierra. Un grafo está formado por un conjunto de vértices (también conocidos como nodos o puntos) y un conjunto de aristas que conectan los vértices. Por conveniencia, definimos un grafo como G = (V, E), donde V representa un conjunto de vértices y E representa un conjunto de aristas. Por ejemplo, V y E para el grafo de la Figura 70 son los siguientes:
V = {"Seattle", "San Francisco", "Los Angeles", "Denver", "Kansas City", "Chicago", "Boston", "New York",
"Atlanta", "Miami", "Dallas", "Houston"};
E = {{"Seattle", "San Francisco"},{"Seattle", "Chicago"}, {"Seattle", "Denver"}, {"San Francisco", "Denver"},
... };
Otros Términos#
Dos vértices de un grafo son adyacentes si están conectados por la misma arista.
Del mismo modo, dos aristas son adyacentes si están conectadas al mismo vértice. Una arista de un grafo que une dos vértices se dice que es incidente en ambos vértices. El grado de un vértice es el número de aristas que inciden en él.
Dos vértices son vecinos si son adyacentes. Del mismo modo, dos aristas son vecinas si son adyacentes.
Un bucle (loop) es una arista que une un vértice consigo misma. Si dos vértices están conectados por dos o más aristas, éstas se denominan aristas paralelas. Un grafo simple es aquel que no tiene bucles ni aristas paralelas. En un grafo completo, cada dos vértices son adyacentes, como se muestra en la Figura 28.3b.
Un grafo está conectado (también conocido como fuertemente conectado) si existe un camino entre cada dos vértices del grafo. Un grafo es débilmente conectado si es conectado cuando se considera que el grafo es no dirigido. Un subgrafo de un grafo G es un grafo cuyo conjunto de vértices es un subconjunto del de G y cuyo conjunto de aristas es un subconjunto del de G.
Supongamos que el grafo etá conectado y no dirigido. Un ciclo es un camino cerrado que parte de un vértice y termina en el mismo vértice. Un grafo conectado es un árbol si no tiene ciclos. Un árbol de expansión de un grafo G es un subgrafo conectado de G, y el subgrafo es un árbol que contiene todos los vértices de G.
Tipos de Grafos#
Un grafo puede ser dirigido o no dirigido. En un grafo dirigido, cada arista tiene una dirección, lo que indica que puedes moverte de un vértice a otro a través de la arista. Las relaciones padre-hijo pueden modelarse mediante un grafo dirigido, en el que una arista del vértice A al B indica que A es padre de B.
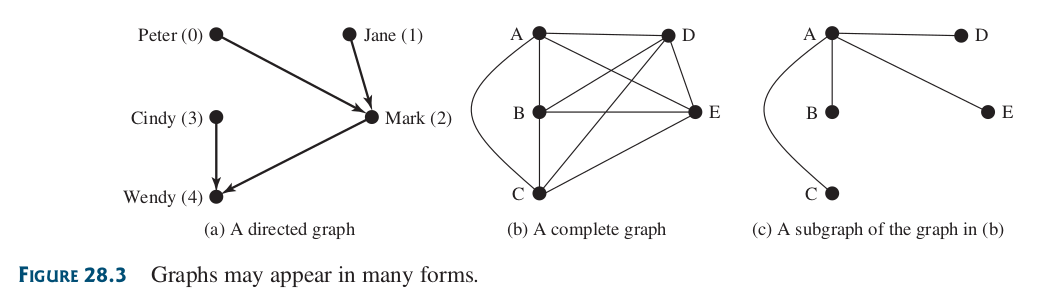
Figura 71 Clasificación de los grafos.#
Representaciones de Grafos#
Existen varias formas de representar grafos en programación. A continuación, se explican las representaciones más comunes:
Lista con las Aristas#
La lista de aristas almacena todas las aristas del grafo como pares de nodos. Es útil para algoritmos que trabajan sobre aristas, como el algoritmo de Kruskal.

Figura 72 Una lista para almacenar los nombres de los vertices.#
Ejemplo#
String[] vertices = {"Seattle", "San Francisco", "Los Angeles",
"Denver", "Kansas City", "Chicago", "Boston", "New York",
"Atlanta", "Miami", "Dallas", "Houston"};
Ahora crea una lista donde los elementos sean objetos de la clase City y tengan los atributos: Nombre, Poblacion, Alcalde.
// Agregar código aquí
Listas de Vertices Adyacentes#
Una lista de adyacencia es una estructura donde cada nodo tiene una lista de sus nodos adyacentes. Es más eficiente en términos de espacio para grafos dispersos.
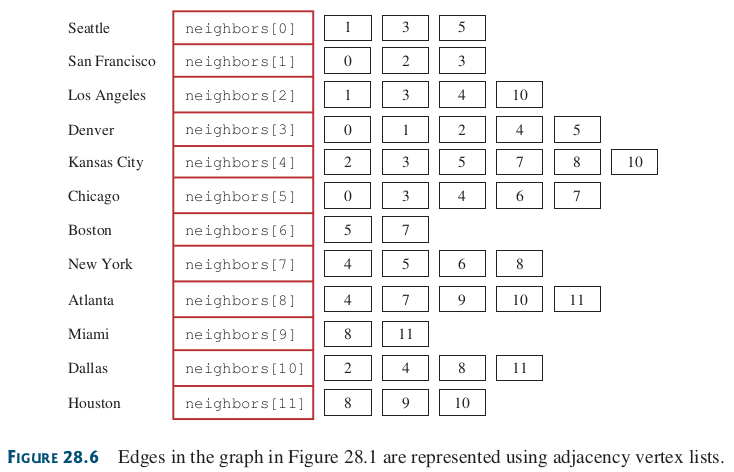
Figura 73 Matriz que guarda los vecinos de cada vértice.#
int[][] neighbors = { {1, 3, 5},
{0, 2, 3},
{1, 3, 4, 10},
{0, 1, 2, 4, 5},
{2, 3, 5, 7, 8, 10},
{0, 3, 4, 6, 7},
{5, 7},
{4, 5, 6, 8},
{4, 7, 9, 10, 11},
{6, 11},
{2, 4, 8, 11},
{8, 9, 10} };
System.out.println(neighbors[0][2]);
5
Listas de Aristas Adyacentes#
Una lista de adyacencia es una estructura donde cada nodo tiene una lista de sus nodos adyacentes almacenados en nodos.

Figura 74 Matriz que guarda los vecinos de cada vértice utilizando la clase nodo.#
Ejemplo#
int[][] edges_USA = {
{0, 1}, {0, 3}, {0, 5},
{1, 0}, {1, 2}, {1, 3},
{2, 1}, {2, 3}, {2, 4}, {2, 10},
{3, 0}, {3, 1}, {3, 2}, {3, 4}, {3, 5},
{4, 2}, {4, 3}, {4, 5}, {4, 7}, {4, 8}, {4, 10},
{5, 0}, {5, 3}, {5, 4}, {5, 6}, {5, 7},
{6, 5}, {6, 7},
{7, 4}, {7, 5}, {7, 6}, {7, 8},
{8, 4}, {8, 7}, {8, 9}, {8, 10}, {8, 11},
{9, 8}, {9, 11},
{10, 2}, {10, 4}, {10, 8}, {10, 11},
{11, 8}, {11, 9}, {11, 10}
};
O, usando la clase de bordes (edges)
public class Edge {
int u, v;
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
public boolean equals(Object o) {
return u == ((Edge)o).u && v == ((Edge)o).v;
}
}
ArrayList<Edge> list = new ArrayList<>();
list.add(new Edge(0, 1));
List<ArrayList<Edge>> neighbors = new ArrayList<>();
neighbors.add(new ArrayList<Edge>());
neighbors.get(0).add(new Edge(0, 1));
neighbors.get(0).add(new Edge(0, 3));
neighbors.get(0).add(new Edge(0, 5));
neighbors.add(new ArrayList<Edge>());
neighbors.get(1).add(new Edge(1, 0));
neighbors.get(1).add(new Edge(1, 2));
neighbors.get(1).add(new Edge(1, 3));
/// ...
true
Matriz Adyacente#
Una matriz de adyacencia es una matriz cuadrada donde cada elemento indica si existe una arista entre dos nodos.
Representar un grafo es almacenar sus vértices y aristas en un programa. La estructura de datos para almacenar un grafo son las matrices o listas.
int[][] adjacencyMatrix = {
{0, 1, 0, 1, 0, 1, 0, 0, 0, 0, 0, 0}, // Seattle
{}, // San Francisco
{}, // Los Angeles
{}, // Denver
{}, // Kansas City
{}, // Chicago
{}, // Boston
{}, // New York
{}, // Atlanta
{}, // Miami
{}, // Dallas
{} // Houston
};
Ahora implementa el código de la matriz adyacente de la figure Figura 83, cambia los elementos del vector de Vertices por objetos de tipo ciudad.
// Agrega aquí el código
Implementación en Java#
Java no trae una clase de grafos implementada. Existen muchas formas de implementar grafos, sin embargo, utilizaremos la clae creada en el libro guía debido a su robustes y completitud.
Esta clase crea la interfaz Graph.java que luego es implementada por los grafos con y sin peso.

Figura 75 Relación entre la interfaz de grafo y las clases de grafo con y sin pesos.#
Las interfaz tiene todos los métodos necesarios que luego son heredados por la clase UnweightedGraph.java. Sin embargo, la clase utiliza dos listas para guardar los vertices y los vecinos.

Figura 76 Diagrama de clase de la interfaz Graph y de la clase genérica de grafo sin pesos, UnweightedGraph.#
Truco
Para ejecutar correctamente las siguientes clases deben ejecutarse en el siguiente orden:
Edge > Graph (saldrá un error de dependencia con UnweightedGraph) > UnweightedGraph > de nuevo Graph > TestGraph > finalmente crear un objeto de la clase TestGraph y ejecutar su método main.
El error que sale es porque Graph depende de UnweightedGraph y viceversa.
// Edge.java
public class Edge {
int u, v;
public Edge(int u, int v) {
this.u = u;
this.v = v;
}
public boolean equals(Object o) {
return u == ((Edge)o).u && v == ((Edge)o).v;
}
}
// Implementa aquí la interfaz Graph.java
// Implementa aquí la clase UnweightedGraph.java
// Implementa aquí una prueba de la clase UnweightedGraph.java, TestGraph.java
// Crear y objeto de tipo TestGraph y ejecutar su método main
Recorridos#
Recorrer un grafo es el proceso de visitar cada vértice del grafo exactamente una vez. Hay dos formas populares de recorrer un grafo: el recorrido en profundidad (o búsqueda en profundidad) y el recorrido en amplitud (o búsqueda en amplitud). Ambas formas dan lugar a un árbol de expansión, que puede modelarse mediante una clase.
Depth-First Search (DFS)#
La búsqueda en profundidad de un grafo parte de un vértice del grafo y visita todos los vértices del grafo en la medida de lo posible antes de retroceder.
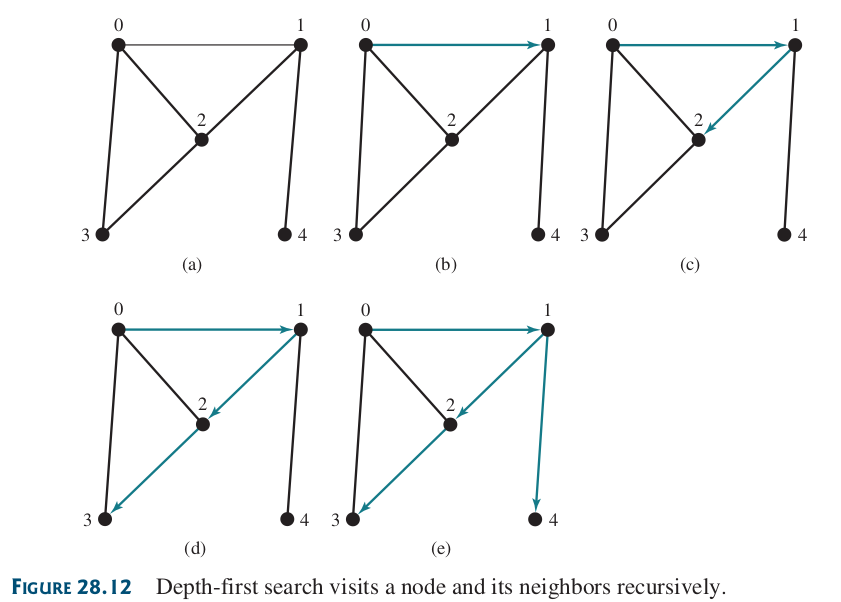
Figura 77 Ejemplo de búsqueda en profundidad para un grafo simple.#
Truco
Se suele utilizar una Pila y un árbol no binario (Spanning Tree) para hacer este recorrido. Al terminar de recorrer todo el grafo la pila debe estar vacía.
// Agrega aquí el código TestDFS.java
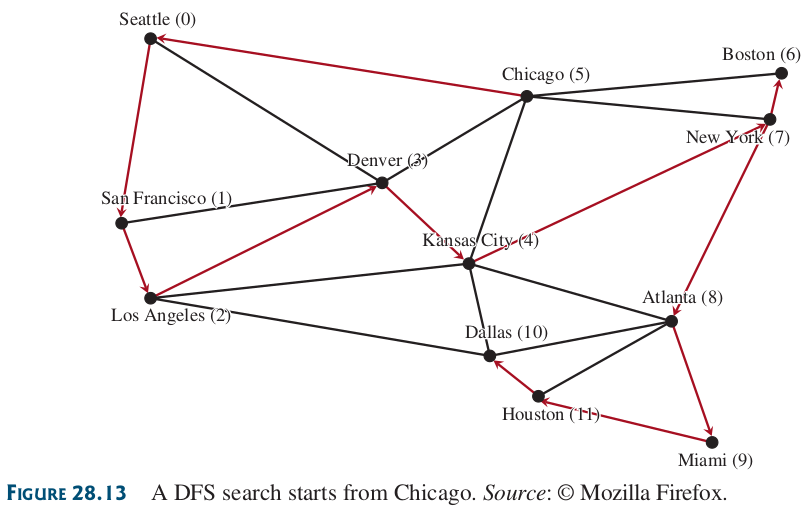
Figura 78 Ejemplo de búsqueda en profundidad para el grafo de EEUU iniciando en Chicago (5).#
Aplicaciones de la DFS#
La búsqueda en profundidad primero se puede utilizar para resolver muchos problemas, como los siguientes:
Detectar si un grafo está conectado. Buscar en el grafo empezando por cualquier vértice. Si el número de vértices buscados es el mismo que el número de vértices del grafo, el grafo está conectado. En caso contrario, el grafo no está conectado.
Detectar si existe un camino entre dos vértices.
Encontrar un camino entre dos vértices.
Encontrar todas las componentes conexas. Una componente conexa es un subgrafo conectado maximal en el que cada par de vértices está conectado por un camino.
Detectar si hay un ciclo en el grafo.
Encontrar un ciclo en el grafo.
Encontrar una trayectoria/ciclo hamiltoniano. Un camino hamiltoniano en un grafo es un camino que visita cada vértice del grafo exactamente una vez. Un ciclo hamiltoniano visita cada vértice del grafo exactamente una vez y vuelve al vértice inicial.
Breadth-First Search (BFS)#
La búsqueda exhaustiva de un grafo visita los vértices nivel por nivel. El primer nivel está formado por el vértice inicial. Cada nivel siguiente está formado por los vértices adyacentes a los vértices del nivel anterior.
Importante
Se deben recorrer, o explorar, todos los vértices adyacentes antes de pasar a la siguiente iteración.
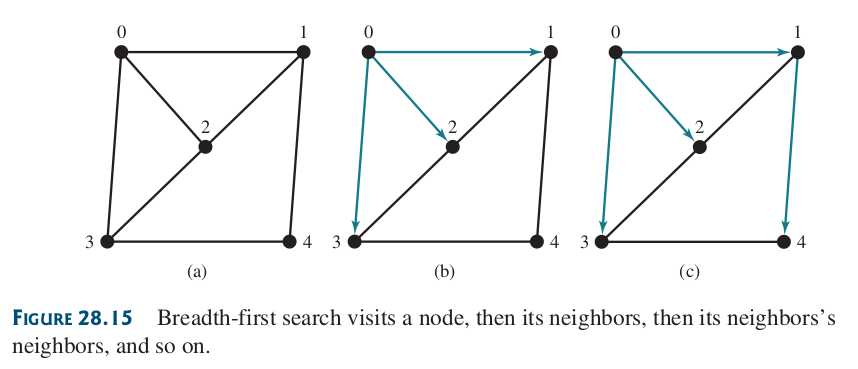
Figura 79 Ejemplo de búsqueda en amplitud para un grafo simple.#
Truco
Se suele utilizar una Cola y un árbol binario (Spanning Tree) para hacer este recorrido. Al terminar de recorrer todo el árbol la cola debe estar llena. Tanto el árbol resultante como el recorrido son de tipo Pre-Order.
// Agrega aquí el código TestBFS.java
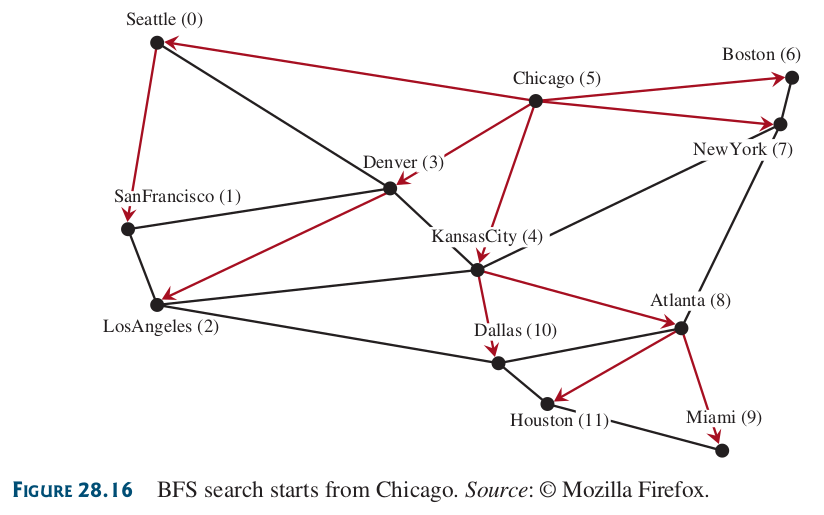
Figura 80 Ejemplo de búsqueda en amplitud para el grafo de EEUU iniciando en Chicago (5).#
Aplicaciones de la BFS#
Muchos de los problemas que resuelve la DFS también pueden resolverse con la BFS. En concreto, el BFS se puede utilizar para resolver los siguientes problemas:
Detectar si un grafo es conectado. Un grafo está conectado si existe un camino entre dos vértices cualesquiera del grafo.
Detectar si hay un camino entre dos vértices.
Encontrar el camino más corto entre dos vértices. Se puede demostrar que el camino entre la raíz y cualquier nodo del árbol BFS es el camino más corto entre la raíz y el nodo.
Encontrar todos los componentes conectados. Una componente conexa es un subgrafo conectado máximo en el que cada par de vértices está conectado por un camino.
Detectar si hay un ciclo en el grafo.
Encontrar un ciclo en el grafo.
Comprobar si un grafo es bipartito. (Un grafo es bipartito si los vértices del grafo pueden dividirse en dos conjuntos disjuntos tales que no existan aristas entre vértices del mismo conjunto).
Conclusión#
Los grafos sin peso son una representación esencial para modelar relaciones entre entidades de manera directa y sin complicaciones. Al no considerar valores asociados a las conexiones, son ideales para problemas donde la prioridad es la topología de la red en lugar del análisis cuantitativo. Comprender su funcionamiento y aplicación es crucial para abordar una amplia variedad de problemas, desde la navegación en redes hasta la simulación de relaciones biológicas. Su implementación en lenguajes como Java ofrece una base sólida para extender su funcionalidad a grafos ponderados y otros modelos más complejos.
Ejercicio#
Taller 7
De la sección de Ejemplos, implementar el viaje por las ciudades (grafo) utilizando la clase UnweightedGraph.java descrita en el capitulo de Implementación en java. Después, recorrer el grafo de forma DFS y BFS utilizando los métodos de las clases. Deben dibujar el grafo utilizando cualquier herramienta de la sección de Visualización.
Deben subir pantallazos de los dos recorridos.
Truco
Primero deben implementar los arreglos de vértices, nodos, y matriz adyacente. La clase de UnweightedGraph.java los requiere (edges y vertices), revisen la sección de Representación de Grafos. Para los vértices deben crear dos arreglos, uno con los nombres de los países y otro donde sus elementos sean de la clase City.