Árboles de Expansión Mínima (MST)

Un árbol de expansión mínima de un grafo es un árbol de expansión con los pesos totales mínimos.

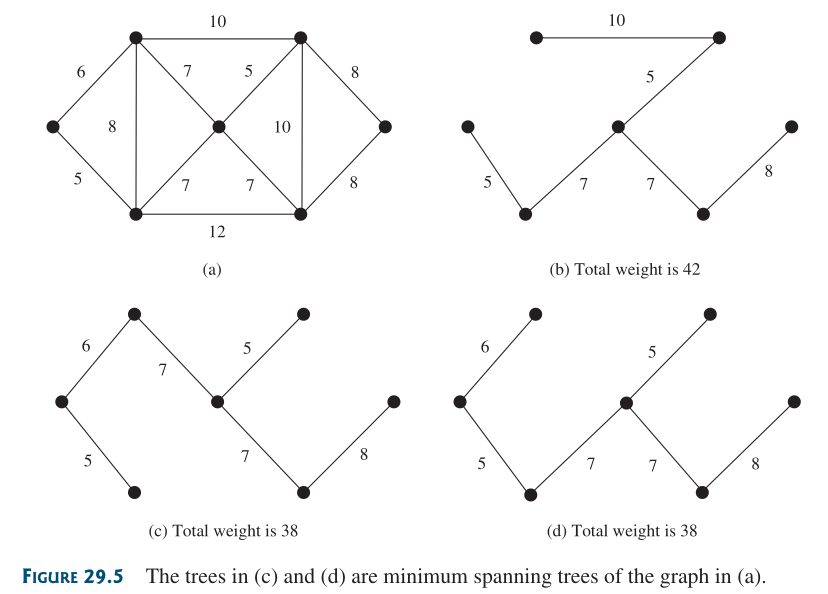
Figura 85 Ejemplos de árboles de expansión mínima para el árbol de la Figura (a).

// TestMinimumSpanningTree.java

Recorridos

Algoritmo del MST de Prim

Algorithm 1 (Prim’s Minimum Spanning Tree)

Entrada: Un \(G = (V, E)\) ponderado no dirigido conectado con pesos no negativos

Salida: MST (un árbol de mínima extensión con el vértice \(s\) como raíz)

MST getMinimumSpanningTree(s) {
      Sea $T$ un conjunto para los vértices del árbol de expansión;
      Inicialmente, añade el vértice inicial, $s$, a $T$;

      While (size of T < n) {
            Encuentra x en T e y en V-T con el menor peso en la arista (x, y).
            Añade y a T y establece padre[y] = x;
      }
 }

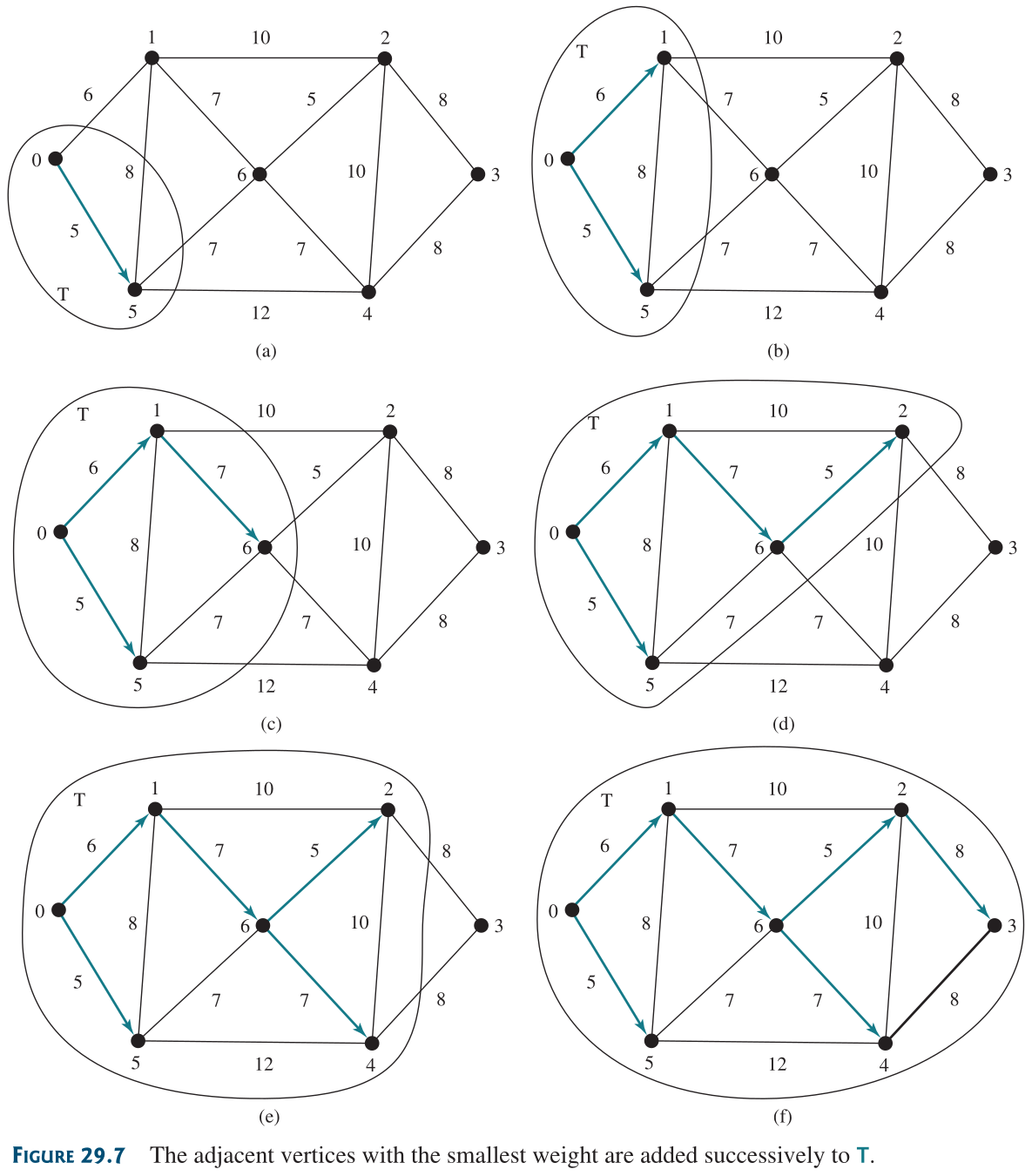
Implementación

// TestMinimumSpanningTree.java

Ejemplo

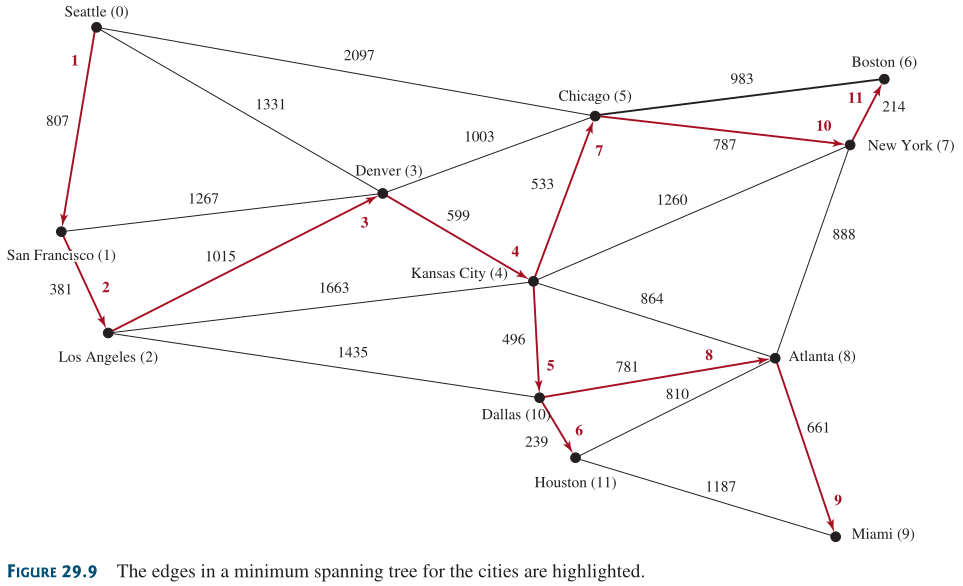
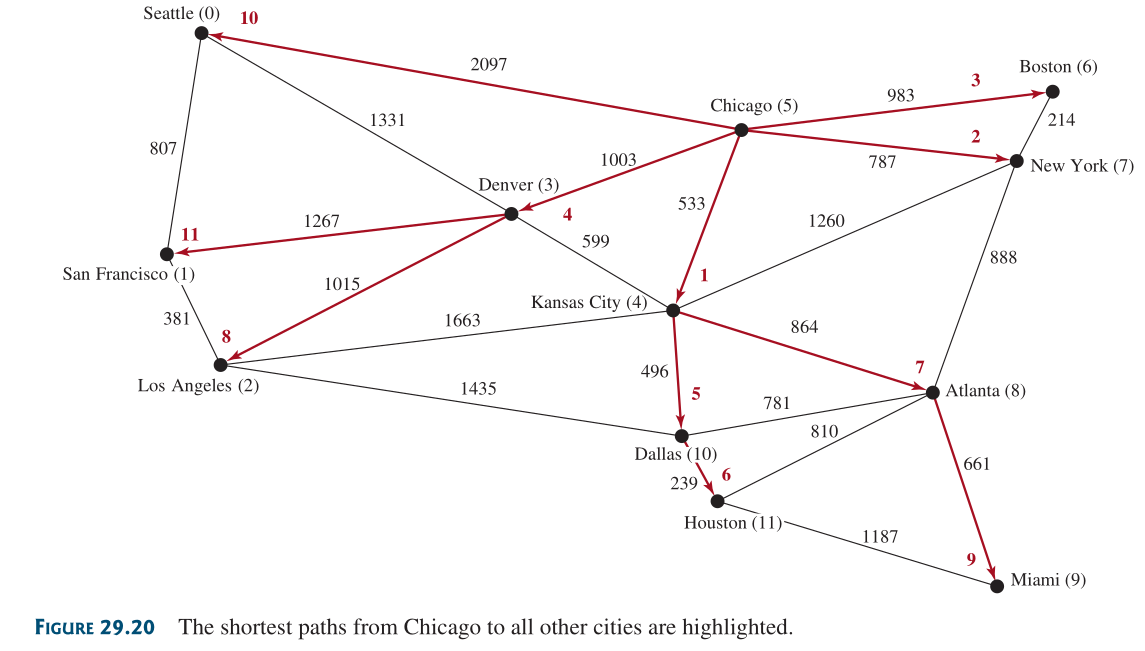
Encontrar el camino más corto

El camino más corto entre dos vértices es un camino con los pesos totales mínimos.

El camino más corto de Dijkstra

Algorithm 2 (Dijkstra’s Single-Source Shortest-Path)

Entradas Dada una red \(G=(V,E)\) con capacidad de flujo \(c\), un nodo origen \(s\), y un nodo sumidero \(t\)

Salida Calcular un flujo \(f\) de \(s\) a \(t\) de valor máximo

ShortestPathTree getShortestPath(s) { Sea \(T\) un conjunto que contiene los vértices cuyos caminos a s son conocidos; Inicialmente T está vacío; Establecer \(costs[s] = 0\); y \(costs[v]\) = infinito\( para todos los demás vértices en \)V$;

While (size of T < n) {
    Encuentra u que no esté en T con el menor costs[u];
    Añade u a T;
    for (each v not in T and (u, v) in E)
    if (cost[v] > cost[u] + w(u, v)) {
      cost[v] = cost[u] + w(u, v); parent[v] = u;
    }
}

}

Implementación

// TestShortestPath.java

Ejemplo